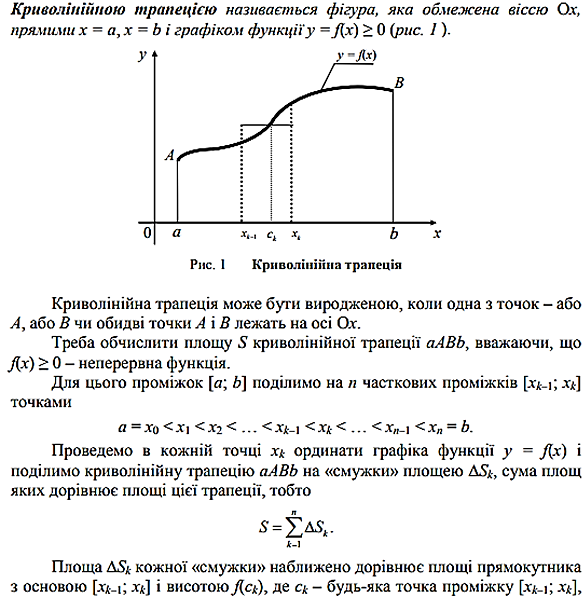
Визначений інтеграл — важлива математична концепція, яка має широке застосування у наукових дослідженнях та технічних розрахунках. За допомогою визначеного інтегралу ми можемо обчислювати площі під графіками функцій, визначати об’єми тіл та розраховувати середні значення величин залежно від їх розподілу.
У фізиці, наприклад, визначений інтеграл дозволяє обчислити роботу, здійснену силами, що залежать від координати, а також знайти шлях, пройдений тілом під впливом сили.
У економіці визначений інтеграл допомагає обчислити вартість товарних запасів, доходи підприємства, а також проаналізувати залежність між виробництвом та витратами.
У біології визначений інтеграл дозволяє розрахувати площу під графіком залежності концентрації речовини в організмі залежно від часу, визначити ефективність лікарських препаратів та багато іншого.
Визначений інтеграл у науці

Визначений інтеграл є важливим математичним інструментом у науці. Він дозволяє розв’язувати диференціальні рівняння, встановлювати функціональні залежності, знаходити значення фізичних величин та робити прогнози.
Один з основних аспектів застосування визначеного інтеграла у науці – це визначення площ під кривими на графіках функцій. Саме таким чином вивчають площі під графіками руху тіл у фізиці, площі під графіками функцій розподілу ймовірностей у статистиці, площі під графіками функцій рівноваги в економічних моделях.
Визначений інтеграл також має використання у статистичному аналізі, де він дозволяє знайти середні значення функцій і визначити ймовірність появи певних подій.
У полярних координатах визначений інтеграл використовується, наприклад, для знаходження площ поверхонь твердих тіл у фізиці, в теорії ймовірностей та в інших галузях науки.
Таким чином, визначений інтеграл має широкий спектр застосувань у наукових дослідженнях та техніці, допомагає з’ясувати відношення між функціями, визначити площі, середні значення, ймовірності та багато іншого. Він є важливим інструментом, необхідним для аналізу та моделювання різних перетворень і явищ у науковому та технічному середовищі.
Застосування визначеного інтегралу у фізиці

Визначений інтеграл має важливе застосування у фізиці, дозволяючи обчислити різноманітні фізичні величини та провести аналіз фізичних процесів.
Одним з основних застосувань визначеного інтегралу у фізиці є визначення площі під залежністю графіка залежності фізичної величини від часу. Наприклад, за допомогою визначеного інтегралу можна обчислити шлях, пройдений тілом протягом певного часового інтервалу або визначити прискорення тіла. Значення визначеного інтегралу дає можливість ознайомитися з описом руху тіла та з’ясувати важливі характеристики.
Крім обчислення величин, визначених графічними залежностями, визначений інтеграл дозволяє обчислити такі характеристики як маса тіла, центр мас та момент інерції. Наприклад, за допомогою визначеного інтегралу можна визначити масу нерівномірно згортаного дроту або маси тіл, що мають нерівномірну густина у просторі.
Також, визначений інтеграл застосовується для вивчення системи зарядів у електростатиці. За допомогою інтегральних виразів можна визначити електричне поле та потенціал, створене системою зарядів, а також обчислити роботу зовнішнього поля у взаємодії зарядів.
Отже, визначений інтеграл є незамінним інструментом у фізиці, дозволяючи чисельно обчислювати різні фізичні характеристики та проводити детальний аналіз фізичних процесів.
Застосування визначеного інтегралу у хімії

Для розв’язання багатьох завдань у хімії необхідно обчислити площу під графіком функції залежності певної величини від часу. Визначений інтеграл дозволяє провести цей розрахунок.
Один з основних прикладів застосування визначеного інтегралу у хімії – визначення концентрації речовини у реакціях. Величина концентрації може змінюватися з часом, і для визначення кількості речовини, що утворюється чи споживається у реакції, потрібно обчислити площу під кривою залежності концентрації від часу.
Також, визначений інтеграл застосовується для визначення об’єму, маси або енергії речовини у різних хімічних системах. В цих випадках, величини залежать від інших фізичних параметрів, таких як тиск чи температура, які також можуть змінюватися з часом.
Застосування визначеного інтегралу у хімії розширює можливості дослідження та вирішення практичних задач в цій науці. Цей математичний інструмент дозволяє отримати точні інформаційні значення та прогнози про кількісні зміни у складних хімічних процесах.
Визначений інтеграл у техніці
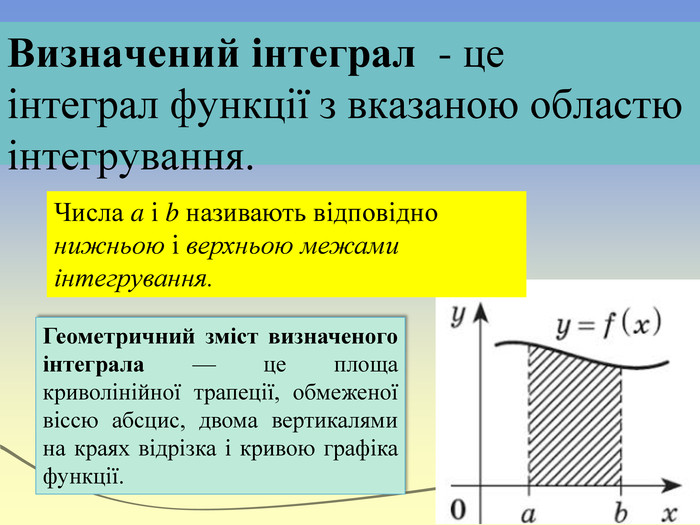
Визначений інтеграл має численні застосування в техніці, допомагаючи вирішувати різноманітні задачі та давати точні результати. Техніка виконується за допомогою математичних моделей, що базуються на рівняннях, що описують фізичні системи. Застосування визначеного інтегралу дозволяє здійснити чисельні обчислення та отримати приблизні значення фізичних величин.
Одним з основних застосувань визначеного інтеграла є обчислення площі під кривою. У техніці це може використовуватися для визначення площі покрівлі, площі огороду або будь-якої іншої площі, забезпечуючи точні результати. Також, цей інтеграл може бути застосований для визначення об’ємів складних форм, що мають неправильну геометрію.
Інше важливе застосування визначеного інтеграла у техніці полягає у визначенні маси об’єктів змінної щільності. Це дозволяє вирішувати задачі зважування та визначення маси складних технічних систем. Наприклад, вимірювання маси літака змінної щільності дозволяє забезпечити безпеку польотів та планувати навігацію.
Крім того, визначений інтеграл може бути використаний для моделювання різних фізичних процесів у техніці, таких як розподіл радіохвиль, теплообмін, механічні коливання та багато іншого. Використання визначеного інтеграла допомагає отримати детальну інформацію про ці процеси та прогнозувати їхні властивості.
Отже, визначений інтеграл виявляється незамінним інструментом у технічних дисциплінах, допомагаючи розв’язувати різноманітні задачі, моделювати фізичні процеси та досягати точних результатів у наукових дослідженнях та практичних застосуваннях.
